DISEÑO DE CIRCUITOS COMBINACIONALES.

Los circuitos combinacionales son un tipo de circuito digital donde las salidas dependen exclusivamente de las combinaciones actuales de las entradas. No tienen memoria (sin elementos de almacenamiento como flip-flops).

Los pasos previos para la construcción de circuitos combinacionales son:

● Construcción de la tabla de verdad a partir del circuito.
● Obtención de las ecuaciones lógicas por minterms o maxterms.
● Simplificación de las funciones mediante Karnaugh o álgebra de Boole.
● Implementación del circuito equivalente con diferentes tipos de puertas o con un solo tipo.

Hasta ahora hemos visto circuitos que disponían de una única salida, pero pueden ser dos, tres o más salidas. Estos circuitos con varias salidas se les conoce como multifunción, ya que están definidos por varias funciones, una por salida. Esto puede ser un problema a la hora de reducir un circuito y, para evitar complicaciones en el proceso de simplificación, es conveniente buscar términos comunes a más de una función para utilizar menos puertas en la fase de construcción.

Cuando construyas la tabla de verdad de un circuito, puede ocurrir que determinadas combinaciones de entrada no puedan producirse o no tengan relevancia y, por tanto, no esté definido el valor que adoptará la salida en este caso. Para estos casos se suele poner una X en la columna de salida (salida indiferente). A la función obtenida se suele llamar función indefinida o función imcompletamente especificada. Hay que tener especial cuidado al realizar la simplificación con Karnaugh, ya que podemos cometer un error.

Entre las características principales de los circuitos combinacionales podemos destacar:

● Sin retroalimentación (feedback).
● Sin reloj (no síncronos)
● Respuesta inmediata (después del retardo de propagación).
● Implementan funciones booleanas.

Circuito detector de números primos.

Cuando se trabajan con circuitos combinacionales, lo primero que hay que definir para establecer la resolución del problema son el número de entradas del circuito digital que estemos intentando simplificar. Además, deberemos de tener claro el número de salidas disponibles para dicho circuito. Y no tanto menos importante, la relación entre entradas y salida, ya que un par de entradas pueden permanecer a una salida o estar conjunta a otra salida.

Por ejemplo vamos a hecer un circuito lógico que detecte números primos del 0 al 7 para evitar que maneje más de 3 bits de información.

Para diseñar este circuito, primero identificaremos cuáles son los números primos en el rango del 0 al 7. Recuerda que, por definición matemática, el 0 y el 1 no son primos. Los números primos en este rango son: 2, 3, 5 y 7.

Como vamos a utilizar un rango de 3 bits, necesitaremos 3 entradas que llamaré A,B y C. Para cada valor de un sistema decimal, en codificación habitual de decimal a binario, pondré los valores en la tabla de verdad. De tal forma que para el primer valor de 0 decimal, los valores de A, B y C serán ceros todos. La salida por lo tanto es cero.

NOTA:Recuerda que traduciendo los valores decimales a bits, con el 0 obtienes el binario 000 (para tres entradas); para el 1₁₀ = 001₂; para el 2₁₀ = 010₂,..., hasta el 7₁₀ = 111₂.

La tabla de verdad queda como ves a continuación:

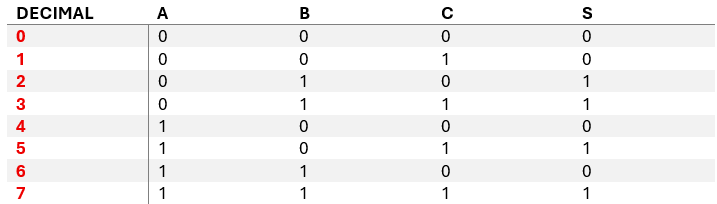
El siguiente paso es sacar las expresiones canónicas de dicha tabla de verdad. Como hay el mismo números de 1 que de 0, sacaremos tanto los minterms y los maxterms de la siguiente forma:

Maxterms.

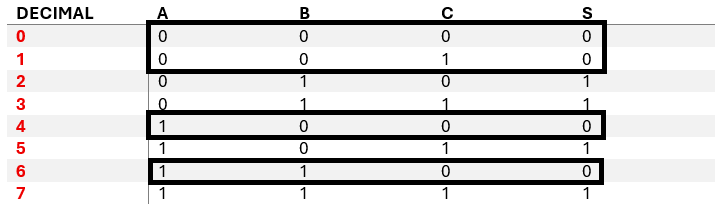
Fmaxterms = (A+B+C)(A+B+C)(A+B+C)(A+B+C)

Basicamente podemos decir que los maxterms se pueden expresar de la forma siguiente con la queivalencia en binario:

● (A+B+C) → 000₂ → M₀
● (A+B+C) → 001₂ → M₁
●(A+B+C) → 100₂ → M₄
●(A+B+C) → 110₂ → M₆

Y la función se escribe como:

F(A,B,C) = ΠM(0,1,4,6)

De los dos primeros términos (A+B+C) y (A+B+C), podemos usar la propiedad distributiva y dejamos los comunes (A+B) en un lado, y en el otro (C + C), en el otro:

(A+B+C)(A+B+C) = (A+B) (CC)

Y como C y su negada se eliminan, nos queda de estos dos términos:

(A+B)

De los dos últimos términos tenemos en común (A+C), por lo que por la misma propiedad:

(A+B+C)(A+B+C) = (A+C) + (B+B)

Por lo que como la variable normal por su negada se elimina, queda entonces los términos:

(A+C)

Si ahora sumamos los resultados (A+B)(A+C), nos queda:

Si operamos algebraicamente nos queda que:

AA + AC + AB + BC. La variable que multiplica a su negada se elimina. Para resolver esto, aplicaremos el Teorema del consenso.

El Teorema del Consenso es una técnica de simplificación en el álgebra de Boole que permite eliminar términos redundantes en una expresión lógica. Es sumamente útil para reducir la cantidad de compuertas necesarias en un diseño digital. Se basa en este contexto:

● Variable y su Negada: Una variable aparece de forma directa en un término (AC) y negada en otro (AB).
● Compañeros de la Variable: Existen otras dos variables (B y C) que acompañan a la variable principal.
● El Término del Consenso: Existe un tercer término formado por esos dos variables (BC). Este es el término que se puede eliminar.

Vamos a comprobarlo mediante la tabla de verdad:

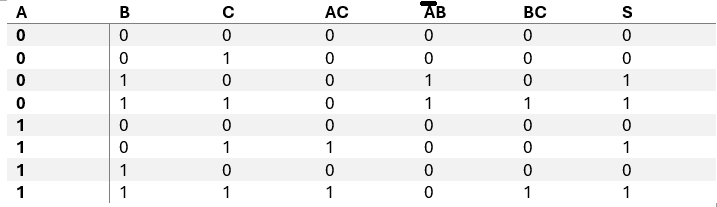
● Para la columna (AC) el valor de A y C deben de ser 1, ya que esta es una puerta AND.
● Para la columna (AB), el valor de A y B deben de ser 1, ya que es otra puerta AND pero ésta con una entrada negada.

Como para la columna (BC) solo se cumple que la salida es 1 para los dos valores que corresponden a AC=1, AB = 0 y AC=0, AB = 1 se puede obviar por lo tanto BC. Este es el teorema del consenso.

Por lo tanto nos queda la ecuación siguiente:

Fmaxterms = AB + AC

Minterms.

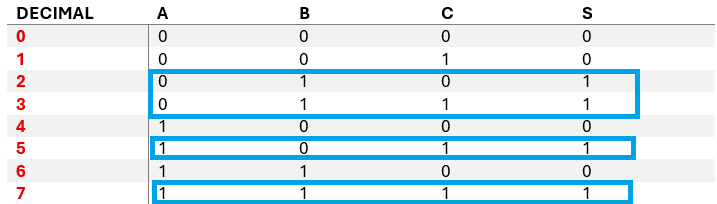
Fminterms = (ABC)+(ABC)+(ABC)+(ABC)

Haciendo lo mismo que en el anterior ejercicio, podemos pasar a binarios los digitos:

● (A+B+C) → 010₂ → m₁
● (ABC) → 011₂ → m₃
● (ABC) → 101₂ → M₅
● (ABC) → 111₂ → m₇

Y la función se escribe como:

F(A,B,C) = Σm(2,3,5,7)

En los dos primeros términos (ABC) y (ABC), se repite la A negada y B, por lo que podemos sacar estas dos variables:

(AB)(C+C)

Del tercer (ABC), y cuarto término (ABC), tenemos en común las variables A y C, por lo que podemos sacarlas de la ecuación:

(AC)(B+B)

De estas dos simplificaciones, las sumas de las variables con su negada es 1, por lo que la ecuación minterms queda como:

Fminterms = AB + AC

Si te fijas tanto la canónica maxterms como la minterms tienen el mismo resultado de función.

Reducción mediante Karnaugh.

Recuerda que Karnaugh es un mapa de tres dimensiones en, lo que primero que hay que hacer es definir las variables del circuito. En este caso hay tres A, B y C. También cogeremos solo los minterms de la tabla de verdad. Por lo que A estará en un lado y BC en el otro lado. Tendremos en cuenta los números a pintar de la siguiente forma:

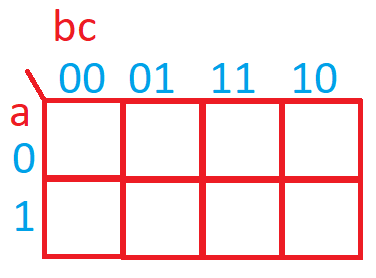
Y teniendo los valores de los minterms:

● m₁ → 010
● m₃ → 011
● m₅ → 101
● m₇ → 111

Nos queda un mapa de Karnaugh siguiente:

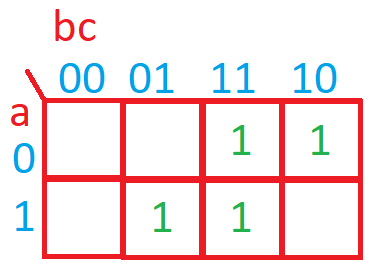
Nos queda agrupar términos. Como se puede ver en la imagen, la agrupación es de dos globos en ambas filas.

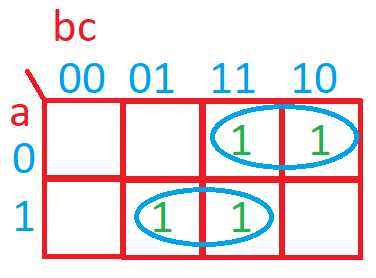
Con lo que en la primera fila nos queda:

ABC
011
010

Siendo comunes la A como negada y la B como normal:

De la siguiente fila tenemos:

ABC
101
111

Siendo comunes la A y la C, por lo que el resultado del mapa queda como:

AB+AC

Que es la ecuación que nos da de cada canónica.

Montaje del circuito.

Es el último paso cuando diseñamos un circuito combinacional. De la ecuación AB+AC, tenemos que una variable negada se está multiplicando por otra variable normal, lo que en esta situación sabemos que es una puerta AND junto con una puerta negada. Además se suma a otra puerta AND de forma que ambas puertas AND están conectadas a una puerta OR y que la salida del circuito dependerán del estado de las entradas.

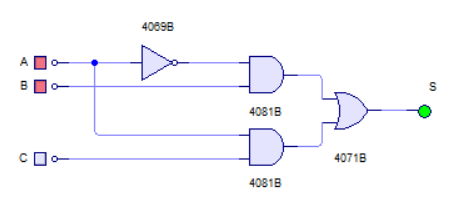
Si aplicas la tabla de verdad original al circuito, verás que las salidas coinciden correctamente:

Así hemos establecido un circuito contador de primos del 0 al 7 tanto en la tabla de verdad como en el circuito físico.

Gracias por compartir el contenido en las redes sociales.